Isotropic systems

In this tutorial, the NMR relaxation times \(T_1\) and \(T_2\) are measured from a bulk polymer-water mixture using NMRforMD. To follow the tutorial, MDAnalysis, numpy, and matplotlib must be installed.

MD system

Measuring the NMR relaxation time from a bulk water-polymer mixture

The system is made of a bulk mixture of 320 \(\text{TIP4P}-\epsilon\) water molecules and 32 \(\text{PEG}300\) polymer molecules. The trajectory was recorded during a \(10\,\text{ns}\) production run performed with the open source code LAMMPS in the NPT ensemble using a timestep of \(1\,\text{fs}\). The imposed was temperature \(T = 300\,^\circ\text{K}\), and the pressure \(p = 1\,\text{atm}\). The positions of the atoms were recorded in the prod.xtc file every \(1\,\text{ps}\).

If you are not familiar with LAMMPS, you can find tutorials here.

File preparation

To access all trajectory and input files, download the polymer-in-water repository from Github, or simply clone it on your computer using:

git clone https://github.com/simongravelle/polymer-in-water.git

The dataset required to follow this tutorial is located in raw-data/NPEG32/.

Create a MDAnalysis universe

Open a new Python script or a new notebook, and define the path to the data files:

datapath = "mypath/polymer-in-water/raw-data/NPEG32/"

Then, import numpy, MDAnalysis, and NMRforMD:

import numpy as np
import MDAnalysis as mda
import nmrformd as nmrmd

From the trajectory files, let us create a MDAnalysis universe. Import the configuration file and the trajectory:

u = mda.Universe(datapath+"init.data", datapath+"prod.xtc")
u.transfer_to_memory(stop=501)

The u.transfer_to_memory(stop=501), is optional, it only serve to reduce the number of frames, and therefore reduce the duration of the calculation. Feel free to remove it, or increase its value. The figures here have been generated using the full trajectory (i.e. without the transfer_to_memory command).

The MDAnalysis universe u contains both topology (atoms types, masses, etc.) and trajectory (atom positions at every frame).

Let us extract a few information from the universe, such as number of molecules (water + PEG), timestep, and total duration:

n_molecules = u.atoms.n_residues
print(f"The number of molecules is {n_molecules}")

>> The number of molecules is 352

timestep = np.int32(u.trajectory.dt)
print(f"The timestep is {timestep} ps")

>> The timestep is 1 ps

total_time = np.int32(u.trajectory.totaltime)
print(f"The total simulation time is {total_time} ps")

>> The total simulation time is 1000 ps

Note that in the context of MDAnalysis, the timestep refers to the duration between two recorded frames, which is different from the actual timestep of \(1\,\text{fs}\) used for the LAMMPS molecular dynamics simulation.

Launch the NMR analysis

Let us create 3 atom groups for respectively the hydrogen atoms of the PEG, the hydrogen atoms of the water, and all the hydrogen atoms:

H_PEG = u.select_atoms("type 3 5")
H_H2O = u.select_atoms("type 7")
H_ALL = H_PEG + H_H2O

Then, let us run NMRforMD for all the hydrogen atoms:

nmr_ALL = nmrmd.NMR(u, atom_group = H_ALL, neighbor_group = H_ALL, number_i=40)

With ‘number_i = 40’, only 40 randomly selected atoms within ‘H_ALL’ are considered for the calculation. Increase this number for better resolution, and use ‘number_i = 0’ to consider all the atoms.

Extract the NMR spectra

Let us access the calculated value of the NMR relaxation time \(T_1\):

T1 = np.round(nmr_ALL.T1,2)
print(f"The total NMR relaxation time is T1 = {T1} s")

>> NMR relaxation time T1 = 2.53 s

The value you obtain may vary, depending on which hydrogen atoms were randomly selected for the calculation.

The full \(T_1\) and \(T_2\) spectra can be extracted as well as 1/nmr_ALL.R1 and 1/nmr_ALL.R2, respectively, and the corresponding frequency is given by nmr_ALL.f.

R1_spectrum = nmr_ALL.R1
R2_spectrum = nmr_ALL.R2
T1_spectrum = 1/R1_spectrum
T2_spectrum = 1/R2_spectrum
f = nmr_ALL.f

The spectra \(T_1\) and \(T_2\) can then be plotted as a function of \(f\) using pyplot.

from matplotlib import pyplot as plt
plt.loglog(f, T1_spectrum, 'o')
plt.loglog(f, T2_spectrum, 's')
plt.show()

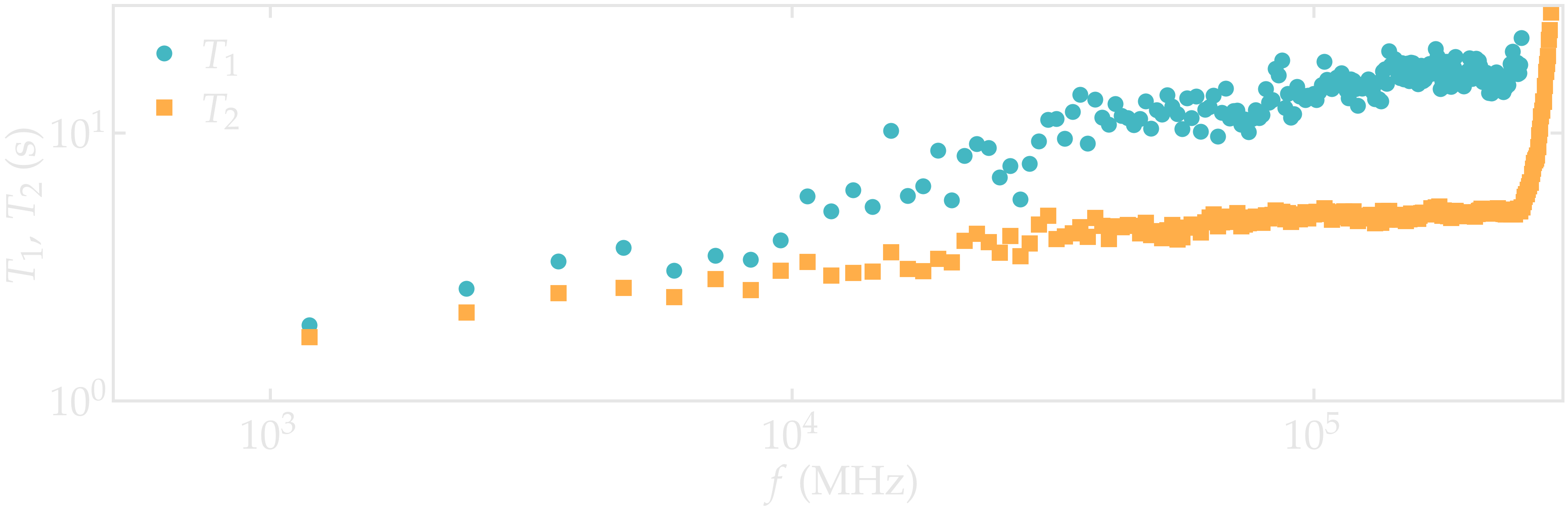
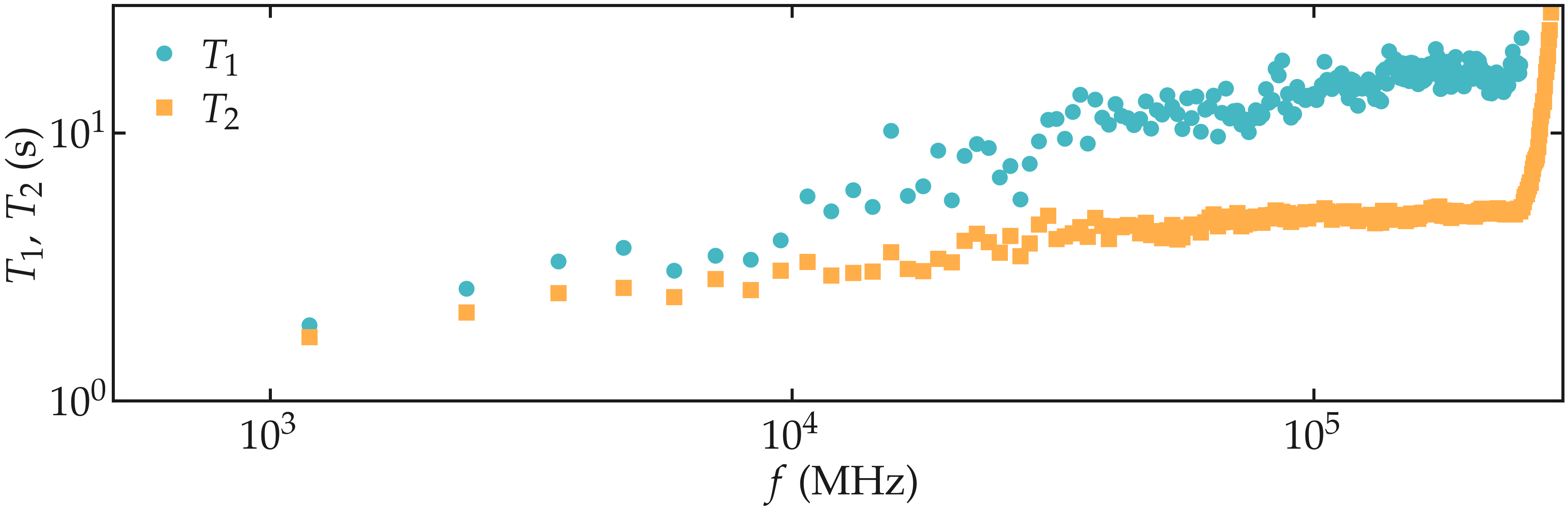
Figure: NMR relaxation times \(T_1\) (disks) and \(T_2\) (squares) as a function of the frequency \(f\) for the \(\text{PEG-H}_2\text{O}\) bulk mixture.

Calculate the intra-molecular NMR relaxation

Let us measuring the intra-molecular contribution to the NMR relaxation time measurement. To make the analysis easier, let us also differentiate between PEG and \(\text{H}_2\text{O}\) molecule, and perform 2 separate analyses.

nmr_H2O_intra = nmrmd.NMR(u, atom_group = H_H2O, type_analysis="intra_molecular", number_i=40)
nmr_PEG_intra = nmrmd.NMR(u, atom_group = H_PEG, type_analysis="intra_molecular", number_i=40)

The correlation function Gij can be accessed from nmr_H2O_intra.gij[0], and the time from nmr_H2O_intra.t.

t = nmr_PEG_intra.t
G_intra_H2O = nmr_H2O_intra.gij[0]
G_intra_PEG = nmr_PEG_intra.gij[0]

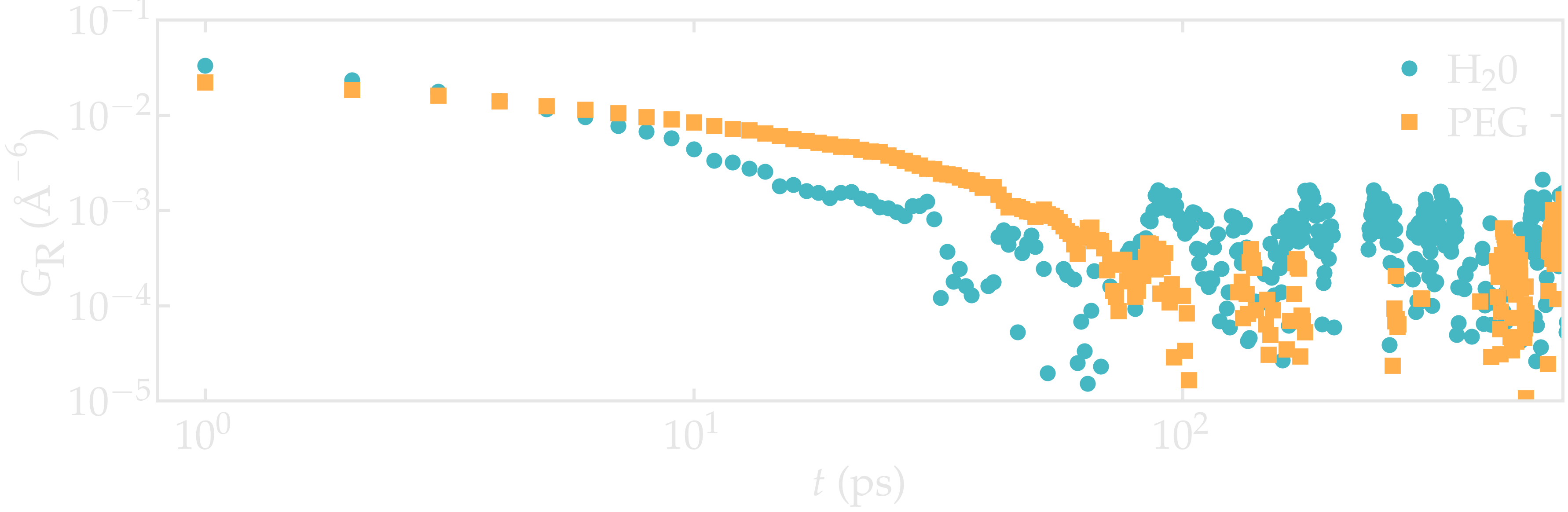
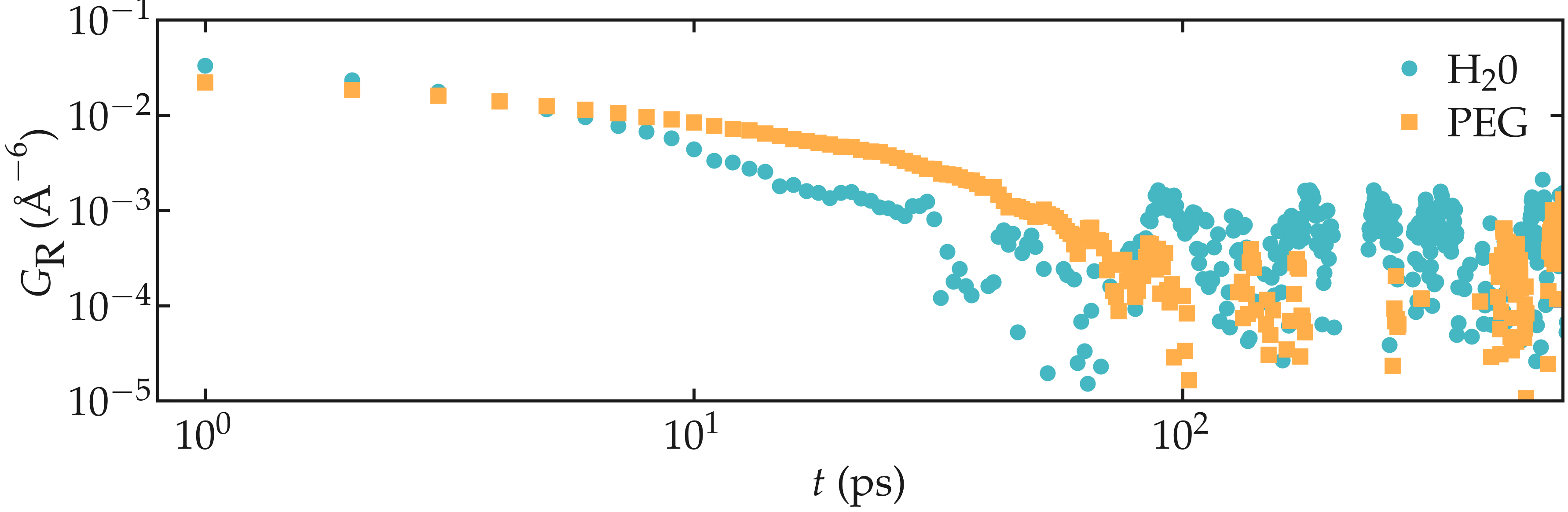
Figure: Intra-molecular correlation function \(G_\text{R}\) for both PEG (squares) and \(\text{H}_2\text{O}\) (disks).

From the correlation functions, one can obtain the typical rotational time of the molecules.

tau_rot_H2O = np.round(np.trapz(G_intra_H2O, t)/G_intra_H2O[0],2)
tau_rot_PEG = np.round(np.trapz(G_intra_PEG, t)/G_intra_PEG[0],2)
print(f"The rotational time of H2O is = {tau_rot_H2O} ps")
print(f"The rotational time of PEG is = {tau_rot_PEG} ps")

>> The rotational time of H2O is = 6.35 ps
>> The rotational time of PEG is = 8.34 ps